概要
こんにちは、すのくろです。
今回は、グラフで時折使う線形回帰式を描画したグラフの作成方法について解説していきます。
線形回帰グラフというのは、下図のようなものです。
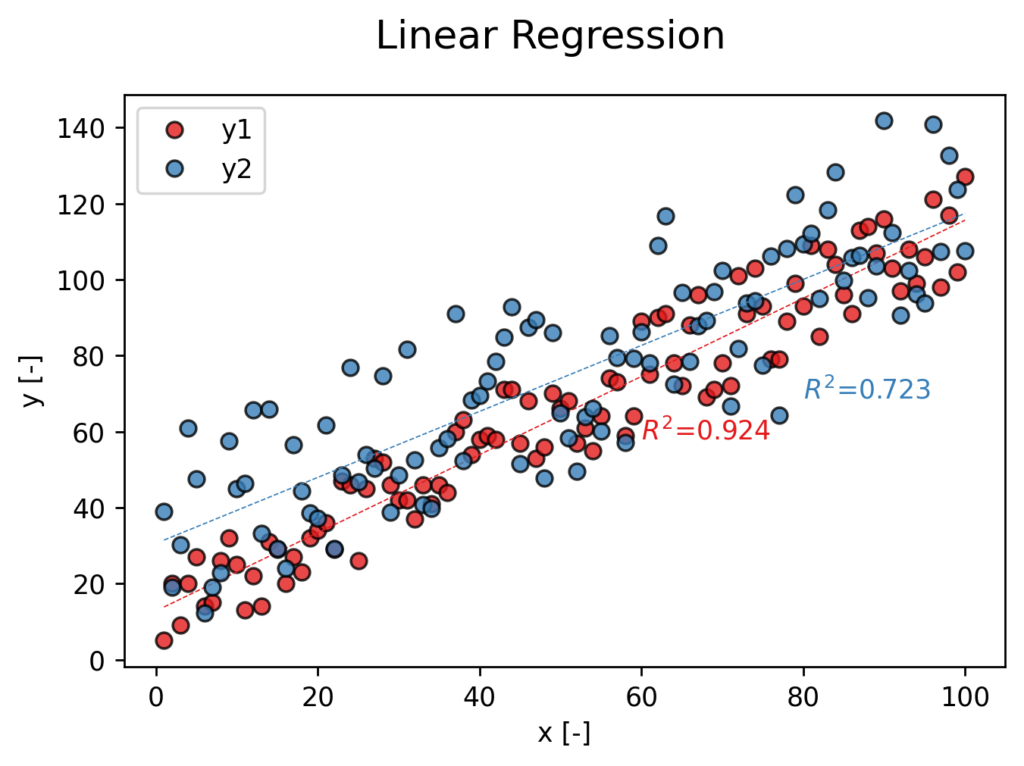
線形回帰グラフはある2変数の関係性の分析や、将来の予測などに活用されます。
pythonを使って↑のように、自分の指定のフォーマットを作っておいて大量のグラフデータを自動で作成できるようになると効率も上がるかと思います。
それでは早速やっていきましょう!
下準備
まずは必要なライブラリをインポートします。
使うのはnumpyなどの基本的なものと、今回の主役である
scikit-learnという科学計算系のライブラリの「LinearRegression」というものです。
コードは下記になります。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.linear_model import LinearRegressionグラフ用データの作成
次にグラフ用のデータを例として作成しておきます。
今回は、2変数xとyを適当に作っておきます。
xは1〜100までの連番です。yはランダムな数を100個作成してます。
# グラフ用データの作成
x = np.arange(1, 101)
y = np.random.randint(1, 30, 100) + x
plt.plot(x, y, "o")
plt.xlabel("x [-]")
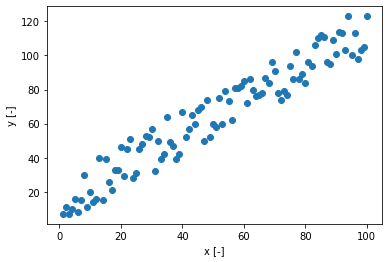
plt.ylabel("y [-]")一応、xとyをプロットすると↓のようなデータ群になります。
xが大きくなるとyが大きくなる傾向です。
今回はこのデータで線形回帰分析をして、グラフ描画していきます。
線形回帰グラフの作成
それでは本題の線形回帰グラフの作成を進めていきます。
全体のコードは下記になります。
# グラフ装飾用カラー
cm = plt.get_cmap("Set1")
# グラフ作成
plt.figure(figsize=(6,4), dpi=250)
plt.suptitle("Linear Regression", size=15)
plt.plot(x, y, "o", mec="k", label="y", color=cm(0), alpha=0.8)
# 線形回帰モデル、予測値、R^2の評価
lr = LinearRegression()
X = x.reshape((len(x), 1))
lr_lin = lr.fit(X, y)
y_lin_fit = lr_lin.predict(X)
r2_lin = lr.score(X, y)
# 予測式の描画
plt.plot(X, y_lin_fit, c=cm(0), lw=0.5, ls="--")
plt.text(X.max()*(0.2), y_lin_fit.max()*0.7, '$ R^{2} $=' + str(round(r2_lin, 3)), c=cm(0))
plt.xlabel("x [-]")
plt.ylabel("y [-]")
plt.legend()
# グラフの保存
plt.savefig("forecast.png")出力結果↓
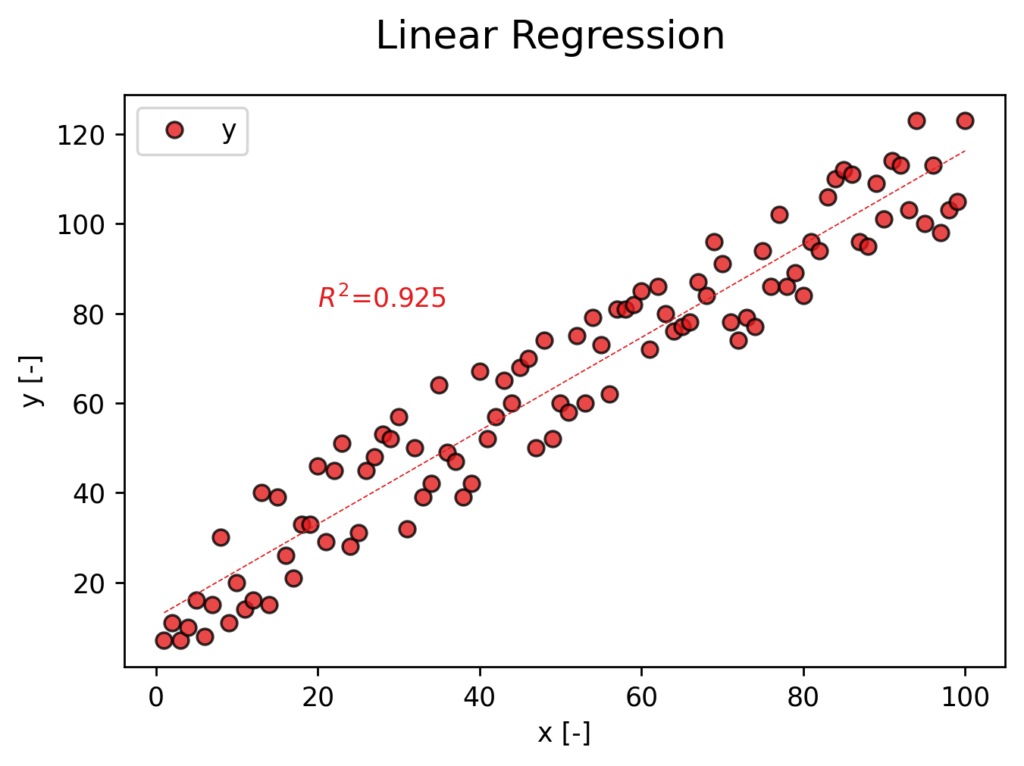
以下で詳細を開設していきます。
グラフの装飾・グラフの作成
初めに、xとyの2変数のグラフを散布図で作成しています。
# グラフ装飾用カラー
cm = plt.get_cmap("Set1")
# グラフ作成
plt.figure(figsize=(6,4), dpi=250)
plt.suptitle("Linear Regression", size=15)
plt.plot(x, y, "o", mec="k", label="y", color=cm(0), alpha=0.8)「cm」は、グラフに使う色を設定していて今回は先ほどのアウトプットでもあるような濃いめの赤い色などが入っている「Set1」を使用しました。
グラフの作成時には、
- グラフの大きさ(figsize)
- グラフの画像の解像度(dpi)
- グラフの上に表示するタイトル(subtitle)
- グラフの描画(マーカーのみ、透明度0.8など)
を設定しています。
この辺りの装飾については他の記事も参考にして頂けると幸いです。
【Python】かっこいい折れ線グラフ(散布図)の作成! | Python for Comfort(新しいタブで開く)
[Matplotlib] 簡単グラフ装飾のデフォルト設定! | Python for Comfort(新しいタブで開く)
線形回帰モデル、予測値、R^2の評価
# 線形回帰モデル、予測値、R^2の評価
lr = LinearRegression()
X = x.reshape((len(x), 1))
lr_lin = lr.fit(X, y)
y_lin_fit = lr_lin.predict(X)
r2_lin = lr.score(X, y)ここのセクションでは、「Linear Regression」を用いて、
まず、線形回帰モデルの作成をします
ライブラリで用意されている「LinearRegression()」を使います。
この「LinearRegression()」の「.fit(X, y)」を使って、xとyの関係性を式にします。
つまり、これが線形回帰モデルの作成になります。
今回の線形回帰モデルを「lr_lin」としています。
次に「lr_lin.predict(X)」を使って再度線形回帰モデルに今回のxのデータを入れて、その時の予測値yを算出します。
それが今回、「y_lin_fit」となります。
最後に、「lr.score(X, y)」でR2値を算出しています。
R2に馴染みのない方に簡単に補足しておくと、R2は「予測式の当てはまり度」となっており、予測した値と元々のyが同じだとR2=1となります。
R2が高いほど、精度の高い予測式となります。
今回は「r2_lin」に「 lr.score(X, y)」で算出したR2値を入れています。
予測式の描画
次に予測式を使って、グラフに破線で線形回帰式を表します。
# 予測式の描画
plt.plot(X, y_lin_fit, c=cm(0), lw=0.5, ls="--")
plt.text(X.max()*(0.2), y_lin_fit.max()*0.7, '$ R^{2} $=' + str(round(r2_lin, 3)), c=cm(0))
予測式は通常の「plt.plot」で、「lw=”–“」で破線で表示しているだけです。
また、この時に「plt.text」でR2値をグラフ内のテキストとして入れています。
テキストの位置(x座標、y座標)は見やすいように、データの最大値などを適当に使って場所を決めています。
グラフの装飾・グラフの保存
最後に、作成したグラフに縦軸、横軸を入れて体裁を整えています。
そして作成したグラフをpng形式で保存しています。
plt.xlabel("x [-]")
plt.ylabel("y [-]")
plt.legend()
# グラフの保存
plt.savefig("forecast.png")ここまでの一連の流れでグラフが完成です!!!
予測式の取得
あとは、予測した線形回帰式の傾きや切片なども知りたいという場合について説明します。
コードは下記になります。
# 予測式の取得
print('傾き = ', lr.coef_[0]) # 傾きを出力
print('切片 = ', lr.intercept_) # 切片を出力
print("予測式: y = {:.2f}x + {:.2f}".format(lr.coef_[0], lr.intercept_)) # 予測式を出力
###出力結果####
傾き = 1.040666066606661
切片 = 12.176363636363625
予測式: y = 1.04x + 12.18これで傾きや切片の値がわかることで、他の分析にも活用することができます。
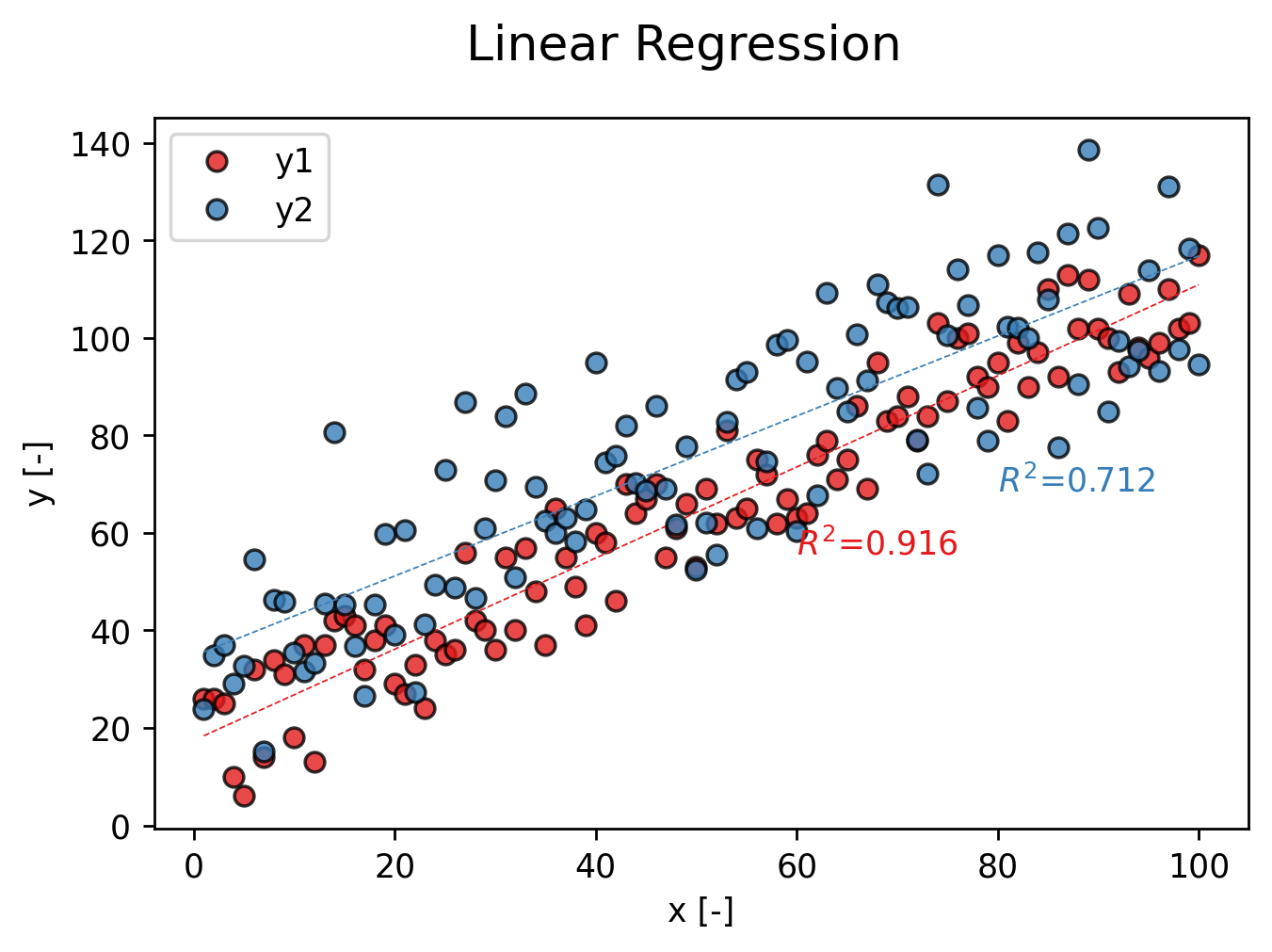
おまけ|複数データ例の場合
同様のやり方でデータが複数ある場合でも、データ「y」に対してfor文を使うことで、
下記のように同じグラフ内でデータのばらつき具合と線形回帰式を表現することも簡単にできるようになります。
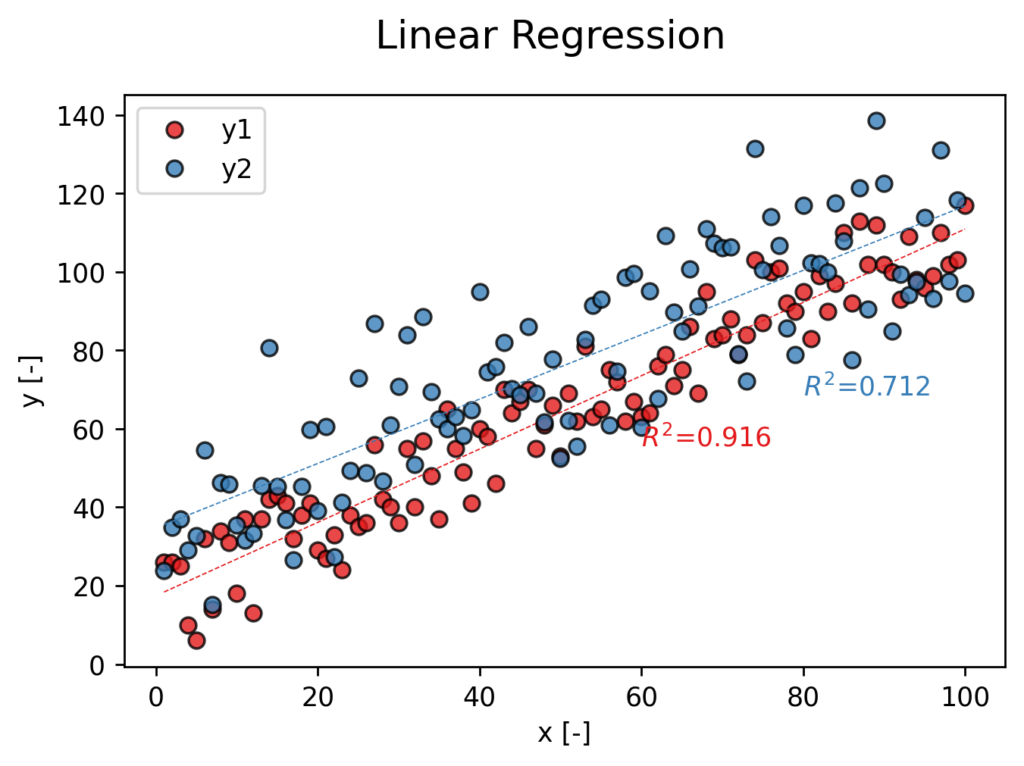
for文の活用方法については他の記事でまとめていますのでこちらも見ていただけると幸いです。
まとめ
今回は線形回帰グラフについて解説しました。
線形回帰式には「Linear Regression」を使ってあげることで、そこまで難しくならずに自分で求めることができました。
今回のようにエクセルだけではなく、Pythonを活用して自分でデータの分析、計算をできるようになっていくと自由度高くかつ、効率的に仕事や研究ができるかと思います!
より、Pythonのスキルを高めて、効率的に業務を遂行したい、高度なPythonを中心としたプログラミングをより体系的に学びたいと言う方向けに、おすすめのオンラインスクールを2つ厳選して紹介していますので、こちらもよければご覧ください!
自分も一度体系的にPythonを学んだことで、一気に日々の業務や人生が変わったと感じています!
以上、ここまでお読みいただき、ありがとうございました!


コメント